Triangulacion Y Propiedades De Los Poligonos Convexos
Un polígono es la región del plano delimitada por una línea poligonal cerrada. Consideremos lo siguiente a Para cada uno de los siguientes polígonos convexos tomen uno de los vértices y desde ese vértice tracen todas las diagonales del polígono.

Triangulacion Optima De Poligono Convexo Programador Clic
Observen la siguiente secuencia de polígonos y sus triangu-laciones para completar la tabla.

Triangulacion y propiedades de los poligonos convexos. Es decir un héxagono por ejemplo tendrá 6 lados 6 vértices 6 ángulos interiores. Sainternos 180n-2 2. Aprender la definición de polígono plano.
Por último en la sesión 4 se busca que aprecien para el caso particular de los polígonos convexos una triangulación más sencilla para este tipo de polí-gonos esto es trazar diagonales desde un solo vértice. Matemáticas II Programa 21 Triangulaciones simples de los polígonos convenxos. Un polígono que tenga n lados la suma de todos sus ángulos interiores es 180 grados n-2 para el cálculo se toma cualquier vértice de referencia y se traza n-2 triángulos.
Los consecutivos y el que no se cuenta. Tenemos dualidad entre los diagramas de Voronoi y la triangulación de Delaunay. El diagrama muestra un diagrama de Voronoi en rojo y su triangulación dual de Delaunay en negro.
Un lado es menor que la suma de los otros dos y mayor que su diferencia. Los triángulos se clasifican según sus lados y según sus ángulos. Primero tendríamos que establecer que el dual de cada teselación tendrá un dual válido.
R s T V MAT2 B3 S21indd 60 91007 123333 PM Propósito de la sesión. Ejemplo 319-2x 140 138 x. En la teoría de la triangulación se prueba que todo polígono admite una triangulación y se establecen algunas propiedades básicas de.
Empezamos dibujando diagonales que partan de un mismo vértice. A esta forma de dividir un polígono en triángulos le llamaremos triángulación simple del polígono. Por lo tanto es una figura con varios ángulos.
Utiliza correctamente los nombres de los polígonos. Propiedades de los polígonos. A este dato se le conoce como n.
Un polígono convexo se puede dividir en triángulos cuyos vértices sean vértices del polígono de tal modo que la suma de las medidas de sus ángulos internos sea igual a la suma de las medidas de los ángulos internos del polígono. Triangulación y propiedades de los polígonos convexos. Definición Diagonal Sean a y b dos vértices de un polígono P se dice que ab es una diagonal de P si y sólo si a y b son claramente visibles entre si.
La palabra polígono está formada por dos voces de origen griego. Observen los siguientes pentágonos y comenten. La suma de los ángulos interiores de un triángulo siempre es 180º.
Teoría de la triangulación. Son polígonos convexos con sus diagonales coincidiendo con los lados. Se llama diagonal de un poligono al segmento determinado por dos vértices no consecutivos.
La suma de todas las áreas de los. Después contesten las preguntas. Triangulación de polígonos convexos 1.
La suma de los ángulos interiores de un triángulo es siempre 180º α β γ 180º. Si tiene dos lados iguales sus ángulos opuestos también son iguales. Sesión 4 Polígono Número de vértices Número de diagonales Número de.
Ahora calculamos el área de cada uno de los triángulos que hemos formado dentro del polígono. Los triángulos son polígonos que tienen 3 lados 3 vértices y 3 ángulos. Cuáles son convexos y cuáles no.
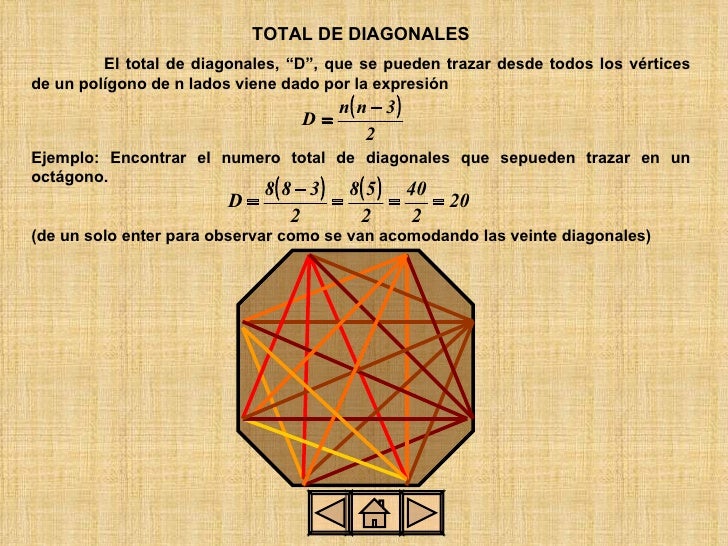
La suma de los ángulos internos de un polígono de n lados se designa como. Triangulacion De Poligonos 1. Propiedad 1 Un polígono convexo de n lados puede ser triangulado en n -2 triángulos trazando las diagonales desde un vértice Ejemplo Propiedad 4 nn-3 2 Un polígono convexo tiene en total diagonales donde n es el número de lados del polígono.
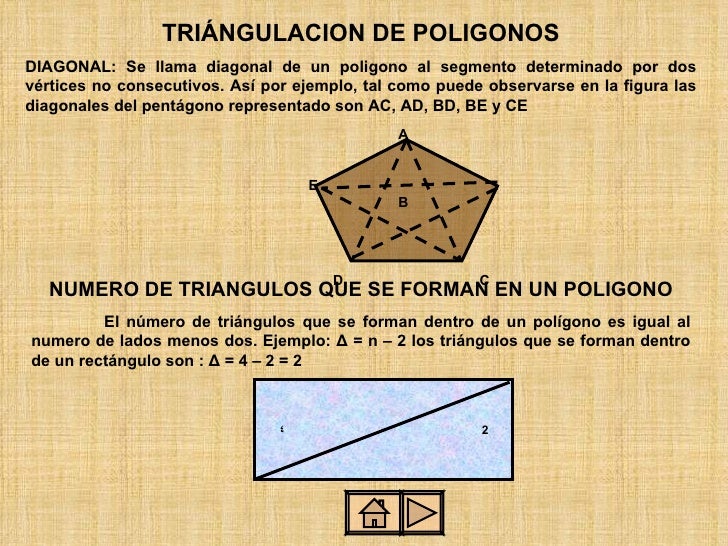
Para calcular el área de un polígono de lados nos apoyaremos en la fórmula para calcular el área de un triángulo. De esta manera se comenzará por decir que los Polígonos convexos pueden ser entendidos como aquellas figuras planas cerradas y delimitadas por segmentos de rectas en las que particularmente se pueden encontrar que todos sus ángulos son menores a 180º mientras que todas sus diagonales también se distinguirán por. TRIÁNGULACION DE POLIGONOS DIAGONAL.
Así por ejemplo tal como puede observarse en la figura las diagonales del pentágono representado son AC AD BD BE y CE A E B D C NUMERO DE TRIANGULOS QUE SE FORMAN EN UN POLIGONO El. Por los tres vértices de los que no salen diagona-les. Reconocer las clases de.
Reúnete con un compañero para analizar qué pasa con la triangulación en el caso de los polígonos convexos. Lo primero que notamos acerca de los dos es que cada borde en el DT es perpendicular a un borde en el VD de hecho los. Vamos a ver ahora algunas de las propiedades de los polígonos.
Las propiedades internas de un polígono corresponde al conjunto de cada uno de sus puntos los cuales se encuentran dentro de la región que delimita esta figura. En un polígono coincide que sus lados vértices ángulos interiores ángulos exteriores y ángulos centrales son iguales.

Triangulacion De Un Poligono Wikiwand

Triangulacion Optima De Poligono Convexo Programador Clic

Triangulacion Optima De Poligono Convexo Programacion Dinamica Programador Clic

Triangulacion De Poligonos Aprende Matematicas
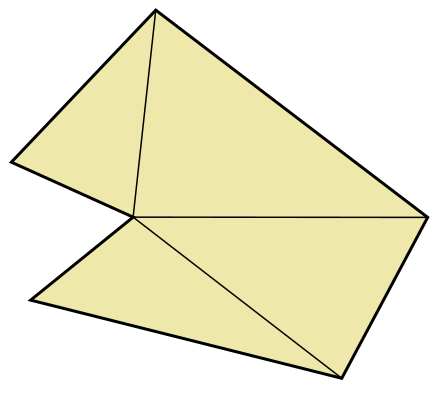
Triangulacion En Abanico Wikiwand
Triangulacion De Poligonos Aprende Matematicas
Triangulacion De Peso Minimo Y Programacion Dinamica

Programacion Dinamica Triangulacion Optima De Poligonos Convexos Programador Clic

Geometria Computacional Tema 4

Clase 1 Triangulacion De Poligonos Unidad Ii Triangulacion De Poligonos Poligonos La Geometria Studocu

Triangulacion Optima De Poligono Convexo Programador Clic

Algoritmo Triangulacion Optima De Poligono Convexo Programador Clic
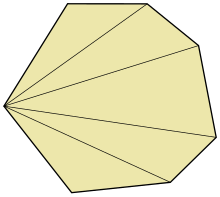
Triangulacion En Abanico Wikiwand

Triangulacion De Un Poligono Wikiwand







Posting Komentar untuk "Triangulacion Y Propiedades De Los Poligonos Convexos"