Definicion De Funcion Periodica
Si es una función periódica de periodo entonces para cualquier entero se cumple que. Serie de Fourier de una función periódica.
FUNCIONES PERIÓDICASUna función periódica f t cumple que para todo valor de t.

Definicion de funcion periodica. Para ysen x el valor máximo es 1 y el valor -1 la diferencia entre el máximo y el mínimo será 2 dado 1--12 por tanto la amplitud se ysen x es A 221 Ejemplo. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. Por lo que es necesario calcular sus transformadas.
Amplitud frecuencia y período. Una función es periódica si los valores de la función se repiten conforme se añade a la variable independiente un determinado período o sea. Se dice que una función f es periódica si para alguna constante P distinta de cero se da el caso de que.
F t f t nT donde n 0 1 2 3Cuestión. F x f x K2 π para todo K Z. Hay diferentes funciones de la forma que se acoplan a ésta descripción porque a y b podrían ser positivos o negativos.
Si el número es el período de la función el número también es un período en el este de la función. Es f t cte. Veamos algunos ejemplos de funciones periódicas.
En matemática una función es periódica si los valores de la función se repiten conforme se añade a la variable independiente un determinado período o sea. Características de las funciones periódicas. Las funciones trigonométricas son funciones muy utilizadas en la ciencia naturales para analizar fenómenos periódicos tales como movimientos ondulatorios corriente eléctrica alterna cuerda vibrantes socilacion de péndulos ciclos comerciales movimientos periódicos de los planetas ciclos biológicos etc.
Donde p es el período una constante distinta de cero y n es un entero positivo. La onda periódica más simple. Si la función periódica con periodo la función también es periódica y su.
Además sen - x - sen x por lo tanto es impar y su representación gráfica es la siguiente. Un químico británico llamado John Alexander Reina Newlands 18381898 fue uno de los precursores de este concepto al proponer la ley de las octavas que indicaba que cada ocho elementos se encuentran propiedades similaresBajo esta idea Newlands elaboró una tabla periódica en 1863. Si es una función periódica se define el periodo mínimo de por.
Es muy común especialmente en aplicaciones ligadas a circuitos elécticos la presencia de una fuerza externa periódica. De la misma manera pero en un contexto físico las ondas periódicas son aquellas ondas que. Teorema Transformada de una función periódica.
Enn otras palabras la gráfica completa puede ser formada de copias de una porción particular repetida en intervalos. Para simplificar el cálculo de los coeficientes de la serie de Fourier de una función periódica dada y además minimizar posibles errores debemos reconocer si la función es par o impar es decir es con respecto al eje y o si posee simetría rotacional con respecto al origen de coordenadas. La tabla periódica o sistema periódico es un esquema que muestra la estructura y disposición de los elementos químicos de acuerdo a una ley de periodicidad la cual consiste en que las propiedades de los elementos son una función periódica de sus números atómicos.
Si ft es una función periódica de. F t f t TAl valor mínimo mayor que cero de la constante T que cumple lo anterior se le llama elperiodo fundamental o simplemente periodo de la funciónObser va que. La Función se llama periódica con un periodo de si alguno de la zona de determinar el número y también entran en el ámbito de la definición y Propiedades periódicas de la función.
Fx sen x sen x 2π sen x 4π sen x 6π. Como la amplitud es esto tiene el efecto de tomar la gráfica de y comprimirla verticalmente por un factor de 2. De la misma manera pero en un contexto físico las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempoes decir describen ciclos repetitivos.
Donde P es el período. Las funciones periódicas son funciones que se comportan en una manera cíclica repetitiva sobre un intervalo especificado llamado un periodo. El conjunto de funciones periódicas de igual período T constituye un espacio vectorial 2.
Si f1t es una función periódica de período nT y f 2t es una función periódica de período mT entonces f 1t f 2t es una función periódica de período mcmn mT. Y en la práctica los coeficientes y se hacen pequeños cuando se. Analice lo que sucede cuando y cuando con.
1 Ejemplo de función periódica. Sen x sen x 2 π sen x 4 π sen x 6 π. Hace grande de manera que cortando la serie por algún valor de grande se obtienen aproximaciones bastante buenas de la solución.
La gráfica se repite a si misma una y otra vez así como es trazada de izquierda a derecha. Vamos a dibujar la gráfica asumiendo que son positivos. PERIODO DE FUNCIONES TRIGONOMÉTRICAS Todas las funciones trigonométricas son periódicas.
Fx cos x. F X PAG F X Displaystyle f x P f x para todos los valores de x en el dominio. La función f x sen x es periódica ya que se cumple que.
Por ejemplo puede escribir la función seno de esta manera. La función tangente fxtg x es también periódica de periodo π. Fx sen x.
Pecado x 2π pecado x n 1 en este caso y el período p para una función sinusoidal es 2π. Una constante P distinta de cero para la cual este es el caso se llama período de la función. En este ejemplo A1 Ω1 y θ0.
Es usual tener voltajes en forma de ondas diente de sierra ondas en escalón etc. Donde P es el período. La prueba quedará como ejercicio.
La función seno tiene un periodo T 2π es decir. El espacio de funciones casi periódicas uniformes en G se puede identificar con el espacio de todas las funciones continuas en la compactación de Bohr de G. La función coseno tiene un periodo T 2π es decir.
De manera más general la compactación de Bohr puede definirse para cualquier grupo topológico G y los espacios de funciones continuas o L p en la compactación de Bohr pueden considerarse funciones casi. Que una función y gt es par si gt gt y una función. La función seno y la función coseno fxsen x y gxcos x son periódicas de periodo π.
El periodo es que es el periodo de.

Matematicas10 Ejemplos De Funcion Periodica
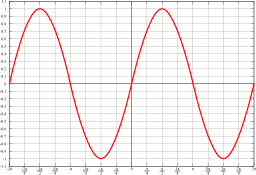
Funcion Periodica Wikipedia La Enciclopedia Libre

Ejemplo De Una Funcion Periodica De Forma Grafica Y Analitica Youtube
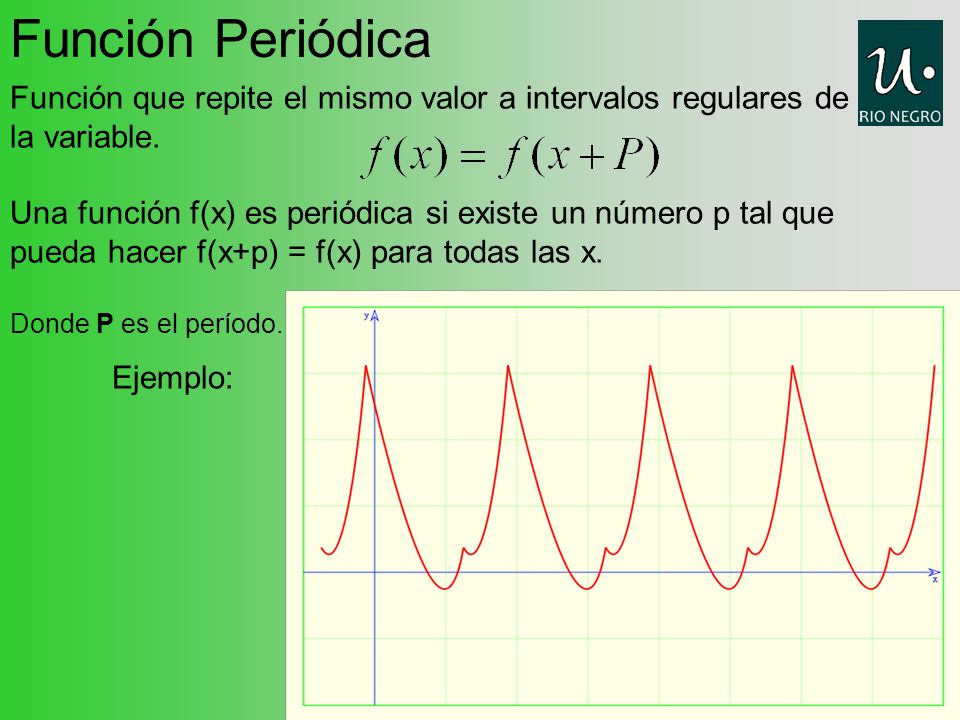
Funciones Definicion Ppt Descargar

Funcion Periodica Wikipedia La Enciclopedia Libre

Matematicas10 Ejemplos De Funcion Periodica
Funcion Periodica Wikipedia La Enciclopedia Libre
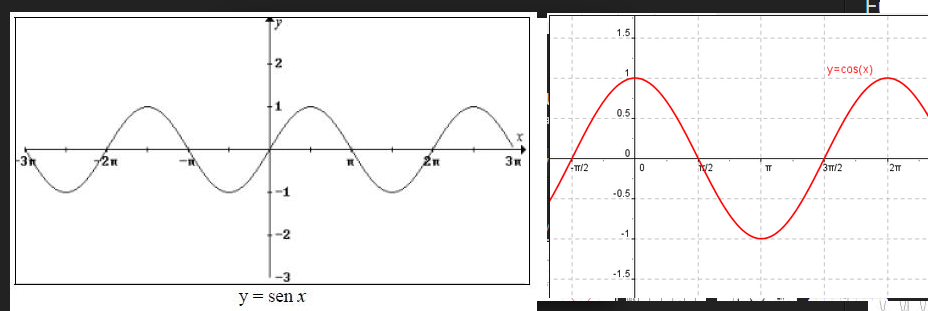
Periodicidad De Una Funcion La Guia De Matematica
3 5 Transformada De La Place De Funciones Periodicas Sierra Exportadora Palta

Funciones Basicas Tema Topicos De Matematica E S C Ciclo Ppt Video Online Descargar

Funciones Ejercicio 4 Periodicidad Youtube

Funcion Periodica I Definicion Youtube

Matematicas10 Ejemplos De Funcion Periodica

Funcion Periodica Wikipedia La Enciclopedia Libre









Posting Komentar untuk "Definicion De Funcion Periodica"